Max-stable processes
Conditional max-stable simulations
Latent Variable
Copula approaches
Miscellaneous
References
Reference Manual
Before introducing the copula framework, I would like to clarify
some points. I'm not "a big fan" of copulas especially when our
interest is to model spatial extremes. Indeed the copula framework
can be misleading since the spatial dependence of extremes might
be falsely taken into account. The extreme value theory suggests
that one should use max-stable copula and this corresponds
actually to consider the finite dimensional distributions of a
max-stable process. However I decided to implement copulas mainly
for educational purposes.
What are copulas?
We introduce copulas by considering the most used copula: the
Gaussian copula. Recall that we are interesting in modeling
spatial extremes and in particular univariate arguments suggest
that block maxima should be well described by a GEV
distribution. If we
denote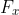 
the
distribution
of )
for
all 
one would write
 \leq y_1, \leq, Y(x_k) \leq y_k] =
\Phi_\Sigma\{\Phi^{-1}(u_1), \ldots,
\Phi^{-1}(u_k)\},
)
where 
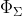is the multivariate Normal distribution with zero mean and
covariance
matrix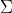 
whose diagonal elements are all equal to
unity,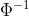 
the quantile function of a standard Normal random variable
and )
for
all 
.
Actually the above equation corresponds to the use of a Gaussian
copula but other copulas can be used by taking for instance the
multivariate Student distribution. Note that the Gaussian copula
is asymptotically independent which implies that the extremes
will occur independently from one location to another one ---
which is not what we really want for spatial extreme don't we?
The Student copula however is asymptotically dependent but tends
to underestimate the spatial dependence of extreme events.
Function "fitcopula": Fit copulas
The density corresponding to the Gaussian copula is easily found
to be
 =
\frac{\varphi_\Sigma\{\Phi^{-1}(u_1), \ldots,
\Phi^{-1}(u_k)\}}{\prod_{i=1}^k
\varphi\{\Phi^{-1}(u_i)\}} \prod_{i=1}^k
f_{x_i}(y_i), )
where 
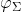is the multivariate Normal density related to
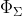and
is the
density related
to 
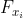. If
one use the Student copula this would give a similar expression
where the Normal densities and quantile functions are
substituted for their Student's analogues.