Any unit Frechet max-stable process can be arbitrarly well approximated by a max-linear model by taking sufficiently large
Max-stable processes
Conditional max-stable simulations
Latent Variable
Copula approaches
Miscellaneous
References
Reference Manual
What is a max-linear model?
A unit Frechet max-linear process is defined by
 =
\max_{j=1, \ldots, p} f_j(x) Z_j, \qquad x \in \mathbb{R}^d,) where
where 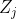 are
independent unit Frechet random variables
and
are
independent unit Frechet random variables
and 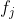 are
non-negative deterministic functions such that
are
non-negative deterministic functions such that
 = 1, \qquad x \in \mathbb{R}^d.)
Any unit Frechet max-stable process can be arbitrarly well approximated by a max-linear model by taking sufficiently large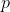 and
suitable
functions
and
suitable
functions 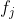 .
.
Any unit Frechet max-stable process can be arbitrarly well approximated by a max-linear model by taking sufficiently large
Function "condrmaxstab": Performs conditional simulations for max-stable processes
Since the
functions 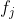 are deterministics, Wang and Stoev [2011] proposed an efficient
algorithm to generate conditional simulations from a max-linear
model and thus approximate conditional simulations from a
max-stable process.
are deterministics, Wang and Stoev [2011] proposed an efficient
algorithm to generate conditional simulations from a max-linear
model and thus approximate conditional simulations from a
max-stable process.
However this approach has some drawbacks since it is not clear how to find appropriate functions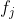 . Therefore
the only available model is currently the (discretized) Smith
model for which
. Therefore
the only available model is currently the (discretized) Smith
model for which
 =
c(p) \varphi(x - u_j ; \Sigma), \qquad x \in \mathbb{R}^d,) where
where ) is the zero mean (multivariate) normal density with covariance
matrix
is the zero mean (multivariate) normal density with covariance
matrix 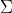 ,
, 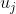 are appropriately chosen points
in
are appropriately chosen points
in 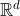 and
and ) is a
constant ensuring unit Frechet margins.
is a
constant ensuring unit Frechet margins.
However this approach has some drawbacks since it is not clear how to find appropriate functions